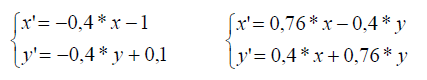smok Heighwaya
Napisano w Zadania
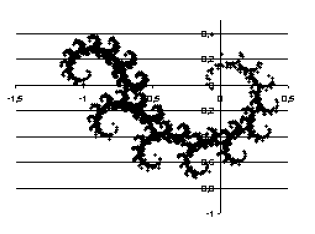
Poniższe dwa układy równań liniowych, zastosowane wielokrotnie do przekształcania współrzędnych punktu (x, y) (10000 razy) na przemian, w losowej kolejności, generują ciekawy obraz, znany jako smok Heighwaya. Zmienne x′ i y′ oznaczają nowe wartości współrzędnych x i y.
smok Heighwaya – wykres
Do wygenerowania obrazu smoka Heighwaya może posłużyć następujący algorytm:
- Przyjmij dowolne wartości początkowe x i y.
- Powtórz wielokrotnie (przynajmniej kilka
tysięcy razy):- Oblicz nowe wartości x i y:
- wybierz losowo z jednakowym prawdopodobieństwem
jeden z dwóch podanych
układów równań, - oblicz x′ i y′ , stosując wybrany układ
równań.
- Zaznacz na wykresie kolejny punkt (x, y).
Wykorzystując dostępne narzędzia informatyczne, wykonaj poniższe polecenia. Wyniki z podpunktów a, c, d zapisz w pliku o nazwie zad_4.txt. Wyniki do każdego podpunktu poprzedź literą oznaczającą ten podpunkt.
- Zaczynając od x = 1 i y = 1 i wybierając za każdym razem losowo jeden z dwóch
podanych układów równań, oblicz pierwsze 5000 wartości x i y z kolejnych iteracji - Na podstawie swoich obliczeń sporządź obraz smoka Heighwaya. Pomiń wyniki
ze 100 pierwszych iteracji. Zadbaj o czytelność i przejrzystość obrazu. Otrzymany
obraz zapisz w pliku o nazwie smok.*, w którym * oznacza rozszerzenie pliku zgodne
z wybranym przez Ciebie formatem pliku użytym do zapamiętania obrazu - Oblicz środek masy smoka, to znaczy: średnie wartości x i y z zaokrągleniem
do jednej cyfry dziesiętnej po przecinku. Przy obliczaniu średnich pomiń wyniki
ze 100 pierwszych iteracji - Oblicz rozmiary powstałego smoka, to znaczy podaj (z zaokrągleniem do jednej cyfry
dziesiętnej po przecinku) minimalne i maksymalne wartości x oraz y. Pomiń wyniki
uzyskane w pierwszych 100 iteracjach obliczeń
Pliki do pobrania
